基本模型
1. 明/密文反馈
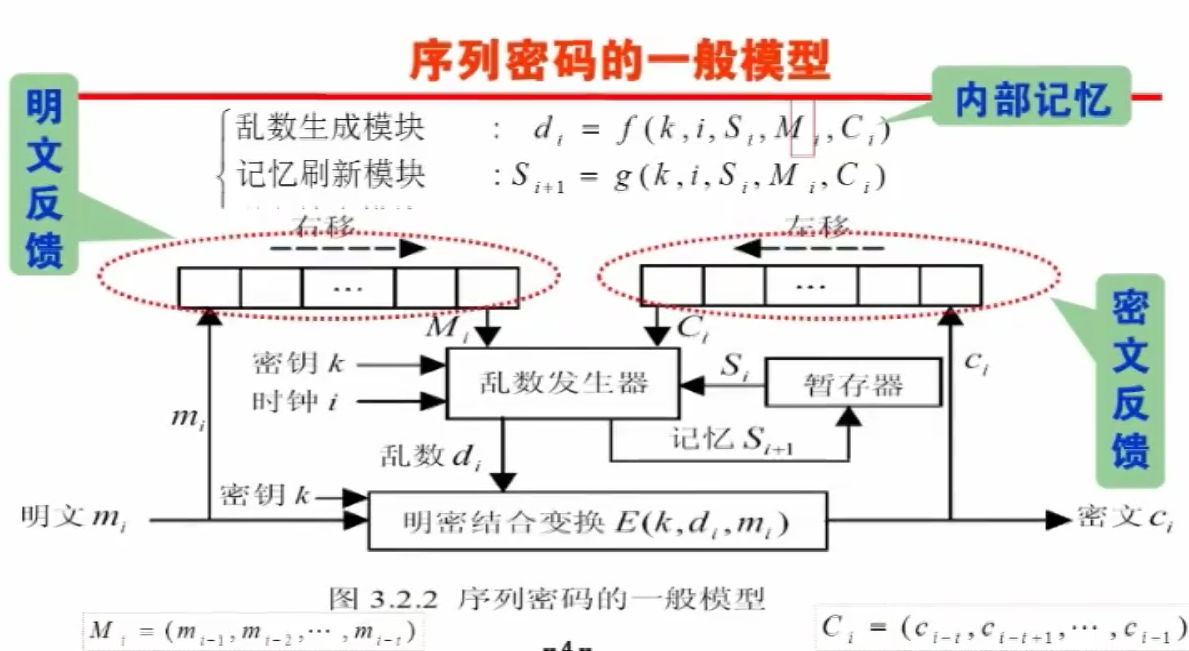
优点:
- 减轻会话密钥重用危害;
- 产生乱数序列一般没有周期;(因为明文一般没有周期)
- 抗破译能力更强;
缺点:
- 信道必须好;(完整性)
2. 无明密文反馈
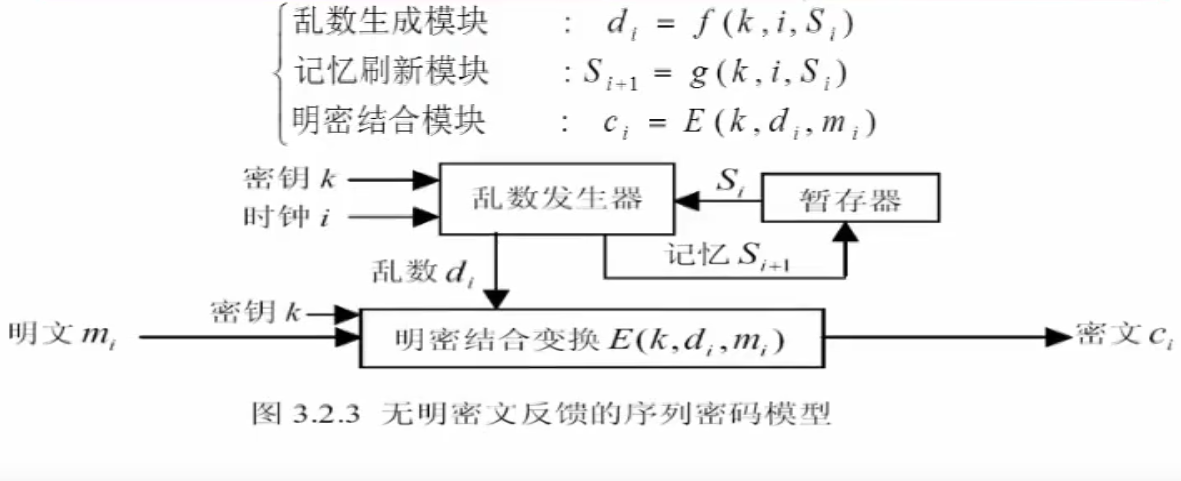
若 和 都不是时钟 的函数,则该模型产生乱数序列一定是最终周期序列。
自同步密码模型
- 一定不是时钟 的函数,与时钟无关;
- 不能有记忆;
- 不能有明文反馈
乱数生成函数只能是密钥和反馈密文的函数。
例:t步恢复的自同步密码数学模型
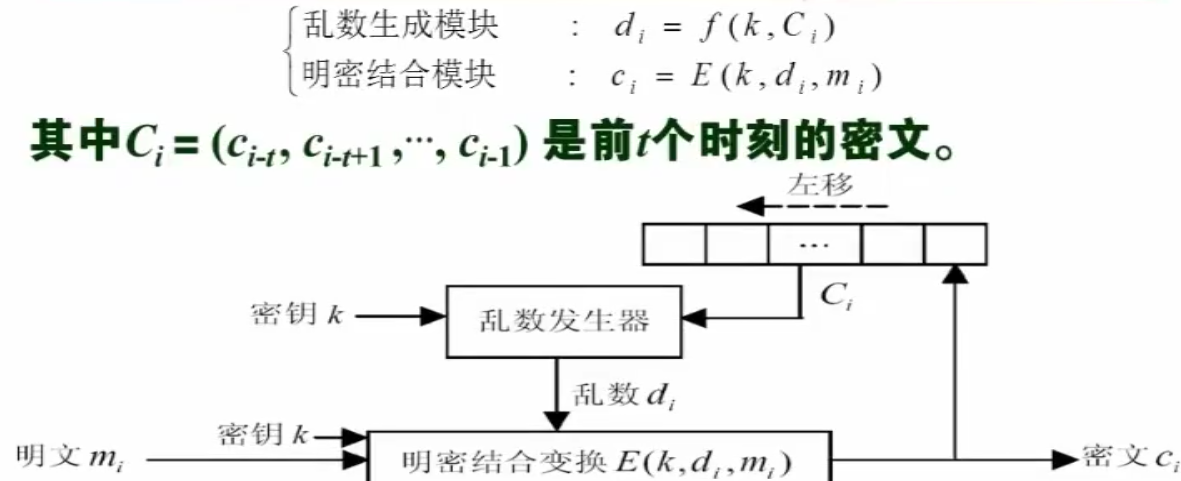
脱密函数:
前馈模型
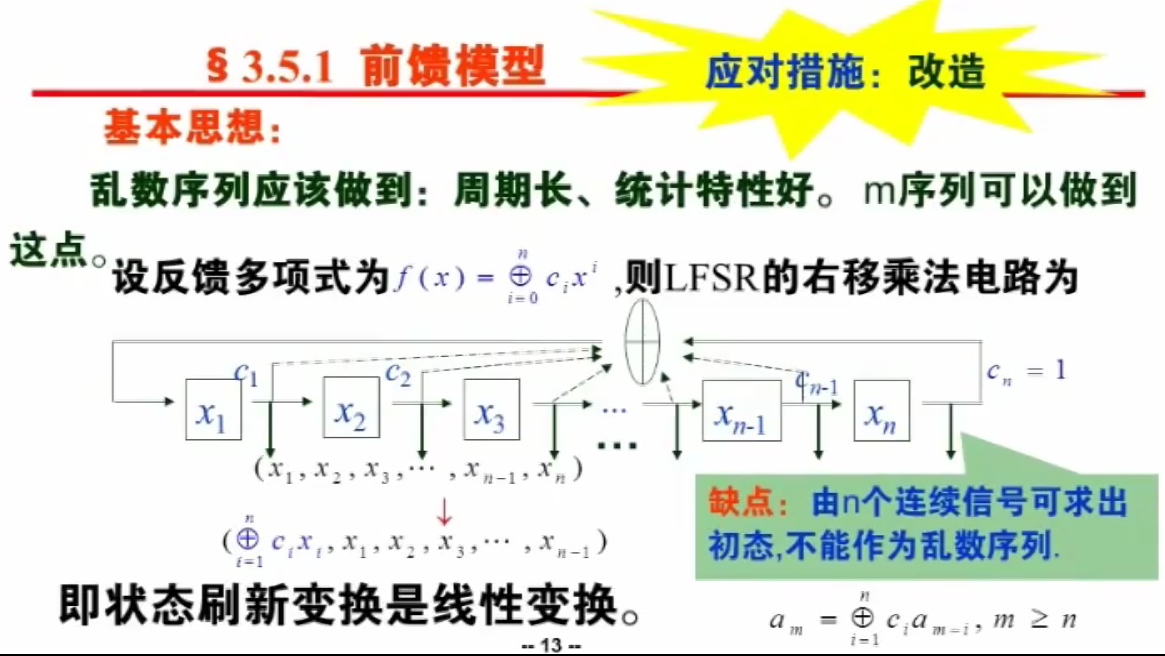
改造即为初始乱源(一个/多个线性反馈移存器或非线性~),加上关于密钥 的非线性变换 。
要求:
- 周期长;-> 乱源输入序列周期长
- 平衡性等伪随机特性好; -> 是平衡函数
- 线性复杂度大(能够产生给定有限长序列最短的线性反馈移存器级数
n); -> 非线性程度高
关键要求:
- 实际找不出乱数序列不随机性;
- 乱数序列求不出密钥;
非线性滤波模型(特殊前馈)
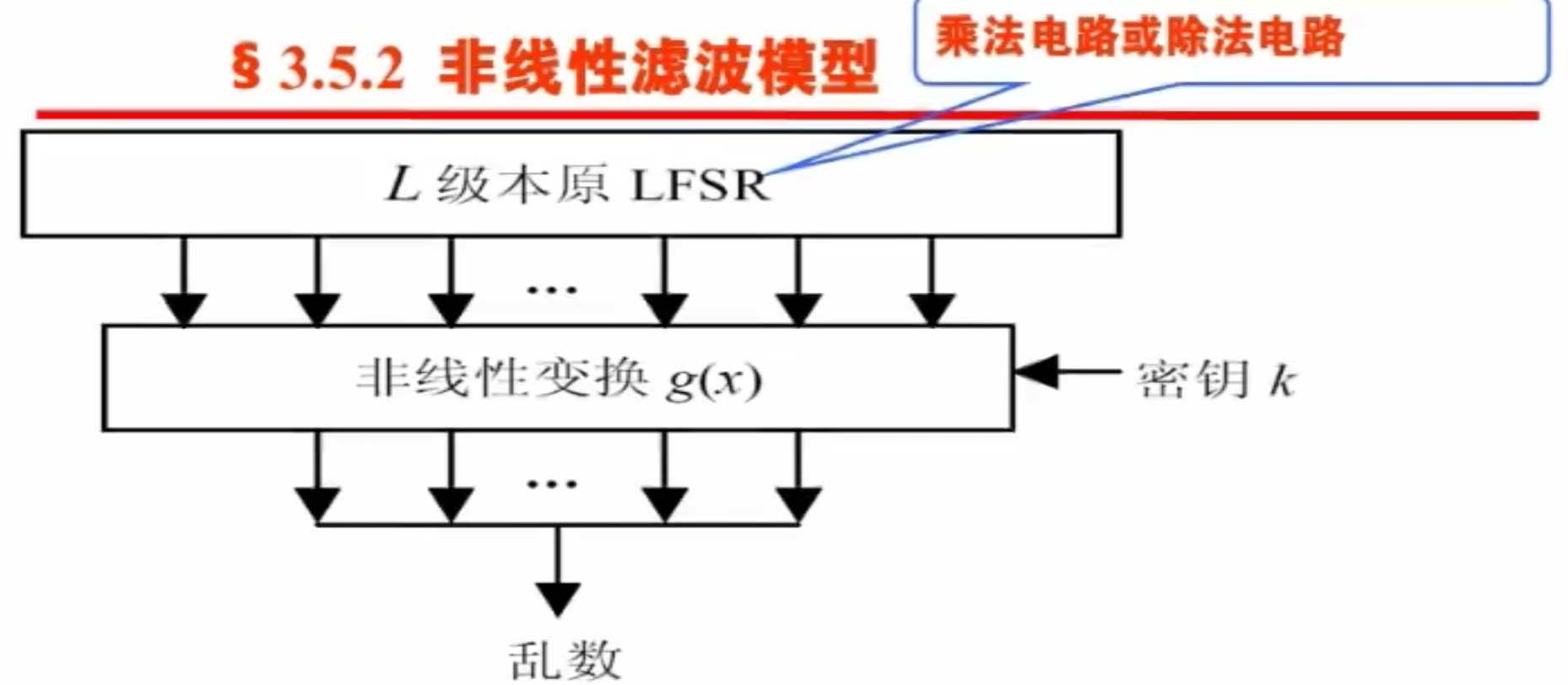
第 时刻输出的乱数:
(平衡特性)由 LFSR 理论可知,在 级 LFSR 状态序列的一个周期内,前馈函数 的 为输入向量 :
- 取非全零向量次数都是 ;
- 取全零向量的次数为 ;
的二元乱序输入序列是平衡函数,则 输出序列也是几乎平衡的, 是平衡函数。
定理3.5.2
设非线性滤波模型由一个级数为 的本源 LFSR 和一个次数为 的非线性 Boole 函数 组成,其中 与密钥无关,则有:
- 乱数序列的线性负载度
- 对任意给定的素数级 LFSR,在次数为 的 Boole 函数集合里随机选 ,它的线性复杂度是最大 () 的概率是
仿射逼近攻击
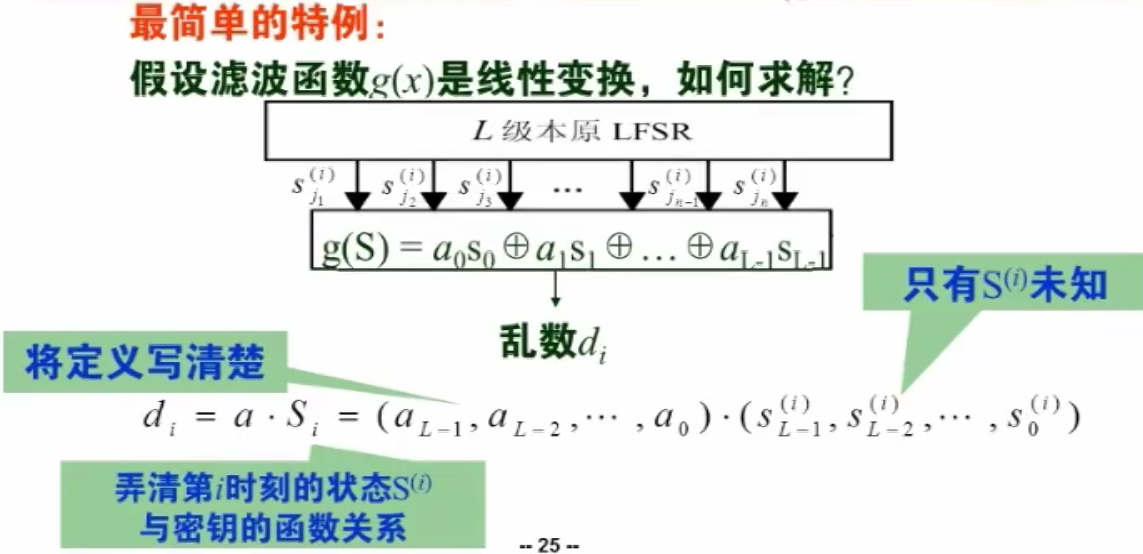
即建立线性方程组求解:
滤波函数 是非线性变换时,通过对其线性逼近,可以由乱数以一定概率得到输入线性组合
由线性组合建立相应方程组。
该方程组为含错方程组,概率 为方程组正确率, 为方程组的优势。
求解采用穷举法,则需要已知乱数个数为 ,穷举量是 。
攻击者希望优势尽可能大,反之亦然。计算的复杂性也和 相关而与 无关。
快速相关攻击法
针对特殊的 LFSR, 如反馈多项式系数非常稀疏时,对于优势很大的含错方程组,可以在多项式时间内求解。
- 攻击者希望优势 尽可能大;
- 设计者希望反馈多项式中的 1 尽可能多;(破坏稀疏系数条件)
结论:
