钟控模型与有记忆变换模型

视频

钟控模型

基本思路：使 LFSR 的动作次数未知化

基本模型：

• 它控
• 自控
• 互控

它控模型

用其它（密钥决定初态的） $L'$ 级本原 LFSR 控制输入 LFSR，也可参与非线性变换干涉乱数生成。

优点：密码性质容易分析

缺点：可穷举控制序列

自控模型

非线性变换不仅产生乱数，还产生控制序列控制输入 LFSR。

优点：抗攻击能力强于它控模型

缺点：密码性质不易分析

互控模型

有许多 LFSR 输入非线性变换，同时每个 LFSR 的控制序列也受其它 LFSR 影响。

优点：更强的抗攻击能力

缺点：密码性质更不易分析

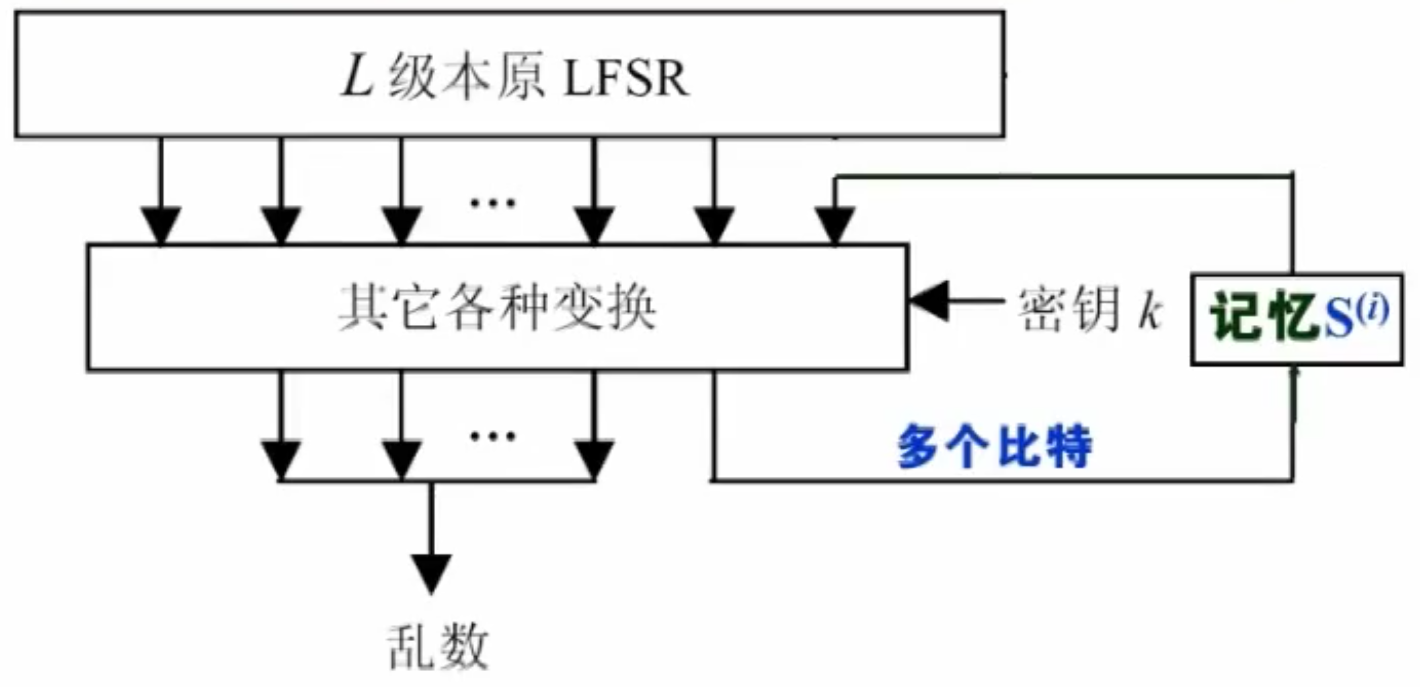
有记忆变换模型

用上一个/几个时刻的计算结果参与当前乱数生成。

$设在 i 时刻输入是 x^{(i)}，记忆是 S^{(i)}，输出是 y^{(i)}。则 \forall i \ge 0，有$

$$\left\{ \begin{matrix} y^{(i)} = f(x^{(i),S^{(i)}}) \\ S^{(i+1)} = g(x^{(i),S^{(i)}}) \end{matrix} \right.$$

一般有记忆变换能增大乱数的周期，有更好的扩散效果、更强抗破译能力。

例：存储-对换变换（RC4）

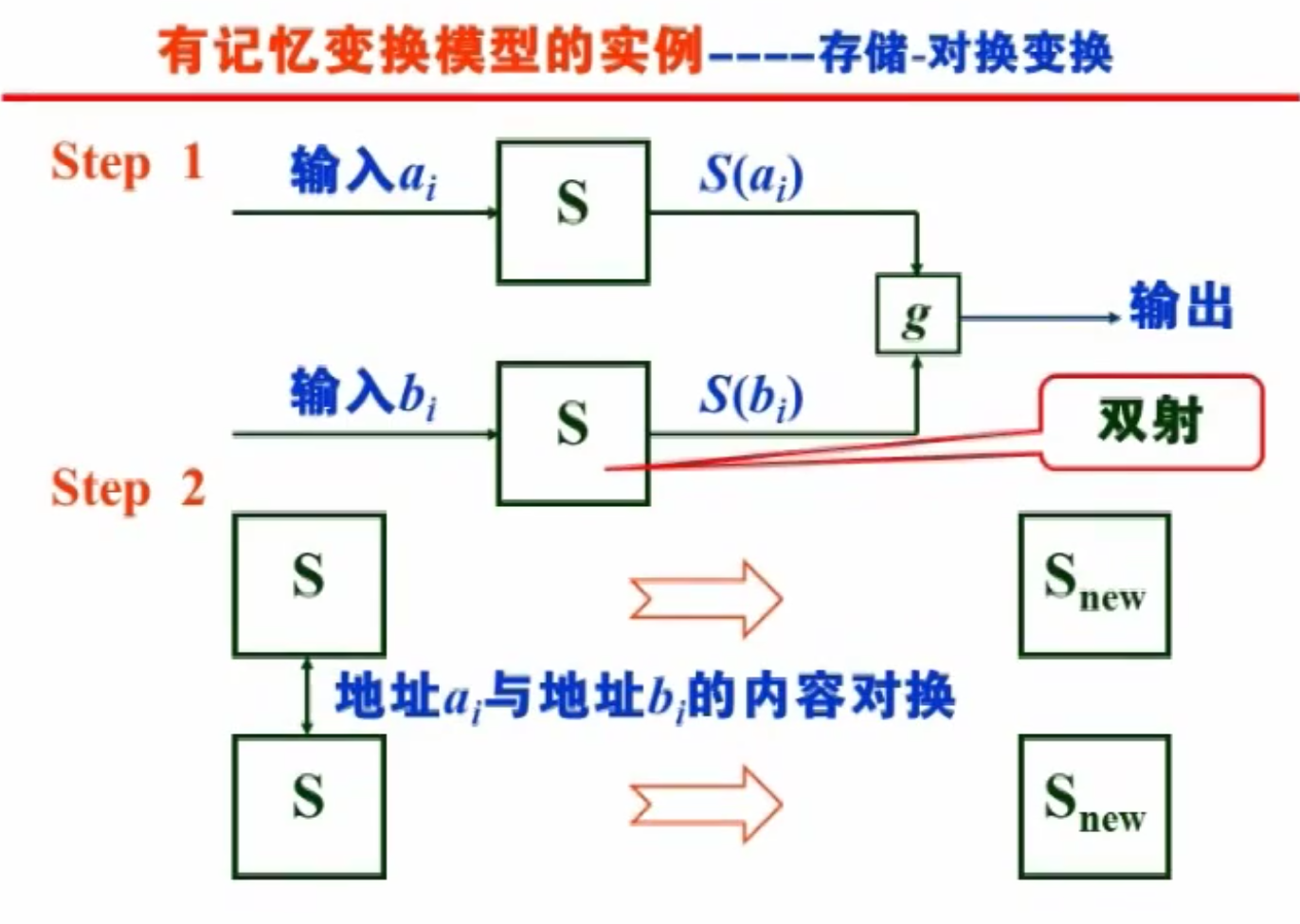
将输入 $a_i, b_i$ 认为是地址，从预设 s 盒中得到相应内容 $S(a_i), S(b_i)$；而后将内容命中的区块对换生成新的 s 盒。

缺点：

1. 变化只有命中的一个区块，$a_i, b_i$ 相同时对换也相同。弱初始 s 盒也可攻击。
2. s 盒的密码特性表现为随机 s 盒，不够好。

问题：怎么设置满足双射的初始 s 盒？

RC4 序列密码算法即为这样的模型。有一个 8 进 8 出的 s 盒，输入输出向量均为 8 维二元向量，s 盒初值由密钥和初始化向量 IV 决定。输出记为 $S(i) = S_i$。

$$(记忆1)S: \{ 0,1 \}^8 \rightarrow \{ 0,1 \}^8$$

有两个计数器$i（时钟）, j（记忆）$，初值均为 0，加密过程中不断修改。

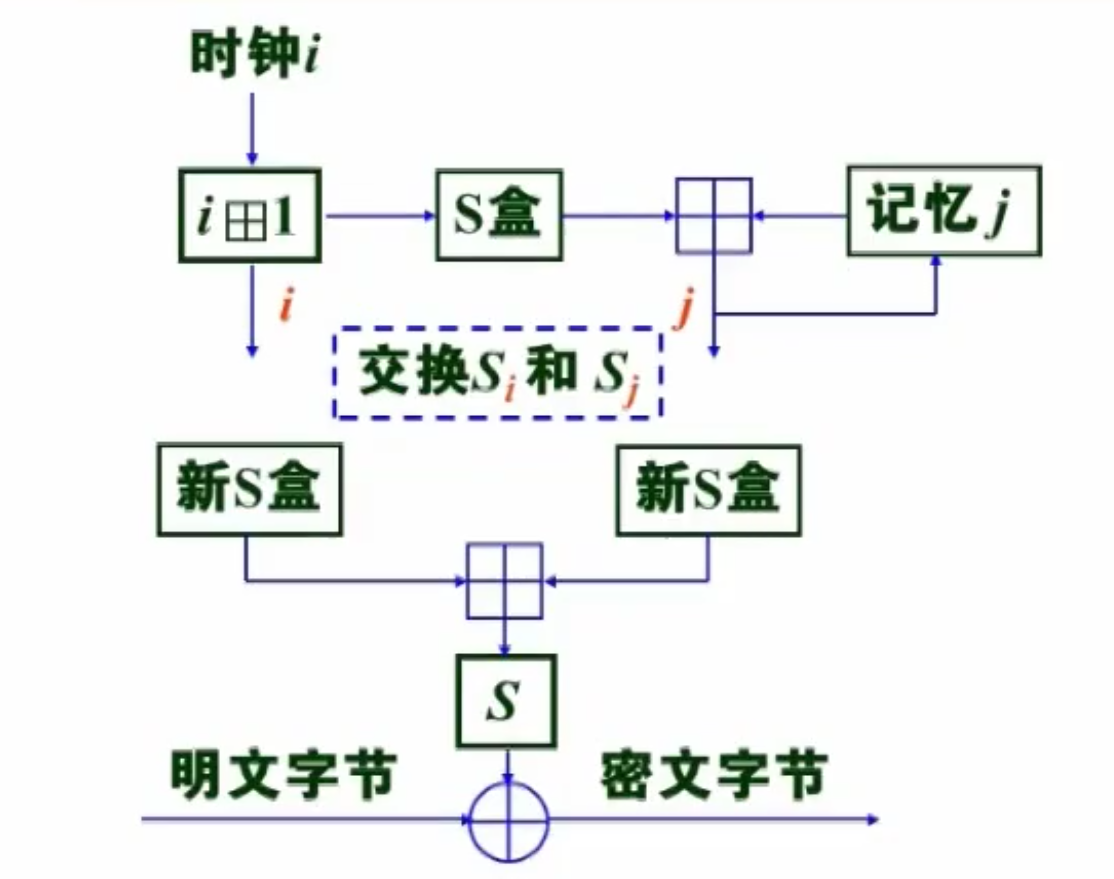
RC4 算法按以下方法产生第 $i 时刻的乱数字节 d_i，完成对第 i 个明文字节 m_i 的加密$。

1. $i = (i+1) mod 256$
2. $j = (j + S_i) mod 256$
3. $交换 S_i 和 S_j$
4. $t = (S_i + S_j) mod 256$
5. $d = S_t$
6. $c = d \oplus m$
7. 返回第一步，对下一个明文字节加密

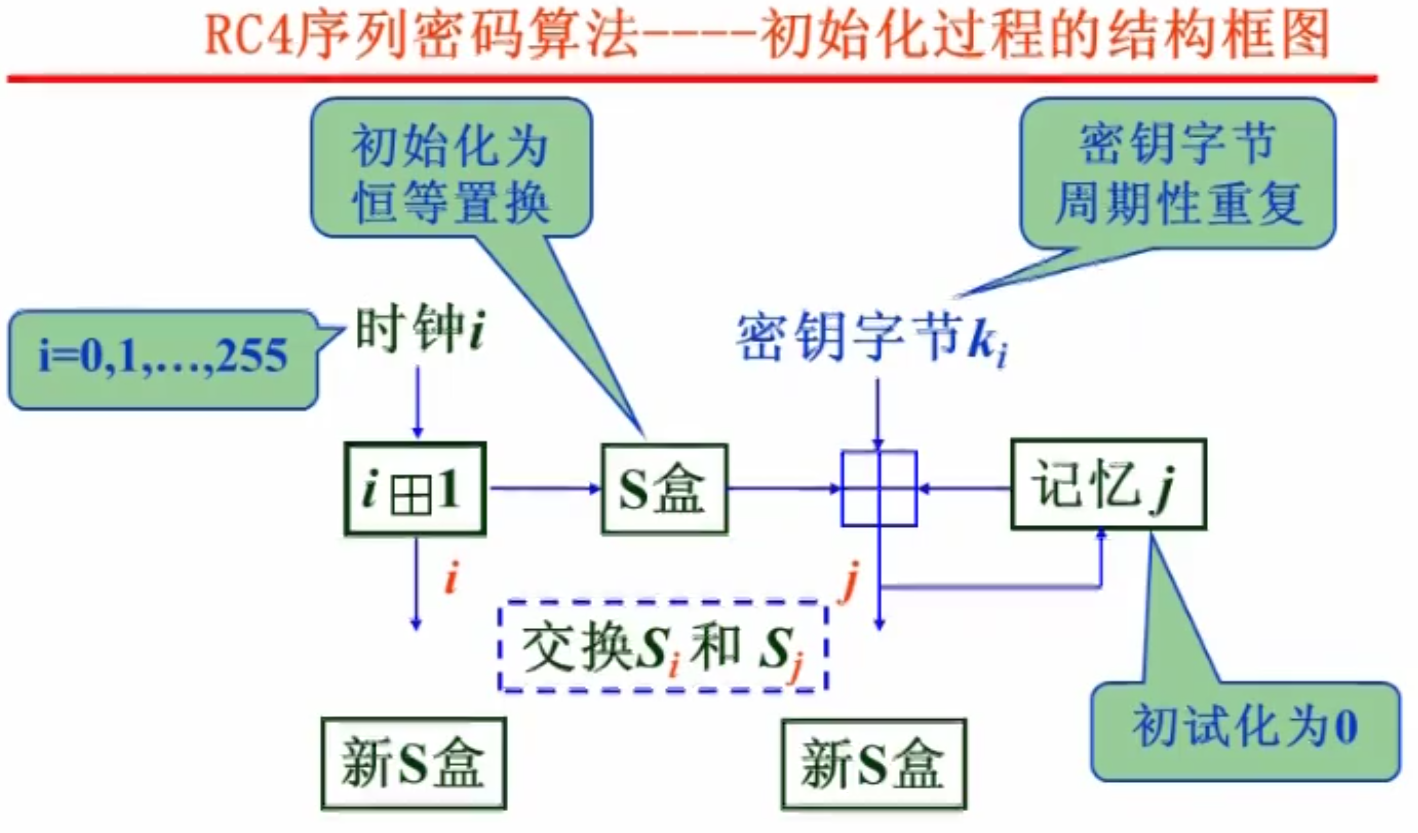
s 盒如何生成？

1. 重复密钥，扩展至256字节，得到 $k_0, k_1, ..., k_{255}$
2. 简单填充 s 盒，$S_i = i$，显然这样是双射
3. $j = 0$
4. for $i$ in range(0,255):
   $j = (j + S_i + k_i) mod 256$
   交换 $S_i, S_j$

RC4 的传递如下。

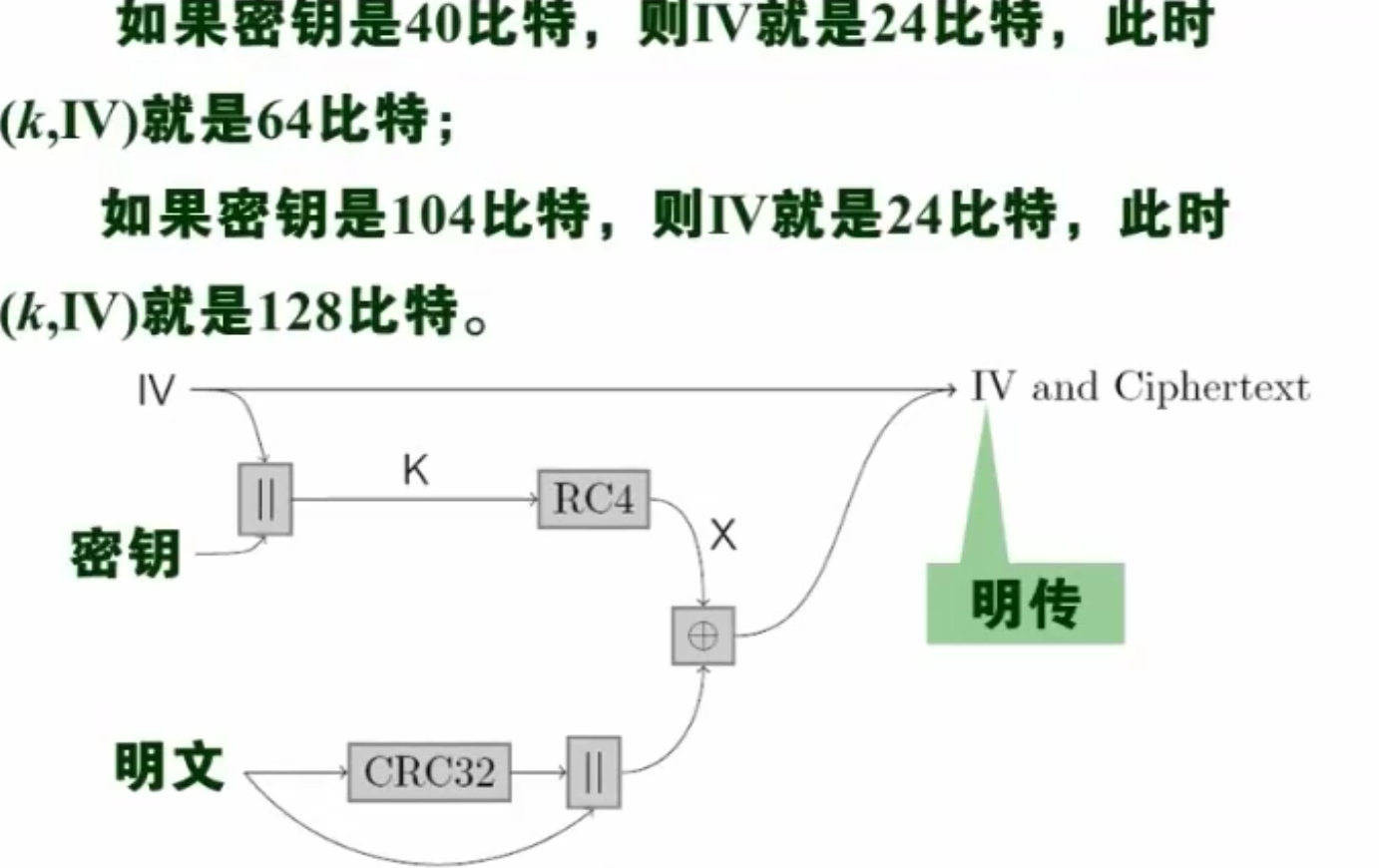
破译：

1. 固定的 s 盒并不安全，连续两个时刻至多有两个地址的值不同，推测 s 盒。
2. 尝试弱 IV 值推测 s 盒。
3. 线性逼近 s 盒，获得密钥与乱数的相关性，统计求解密钥。（用 $i 和 S_j 逼近 j$）