非线性组合模型

视频

非线性组合模型就是多个线性反馈移存器（LFSR）为一个非线性变换提供输入变量

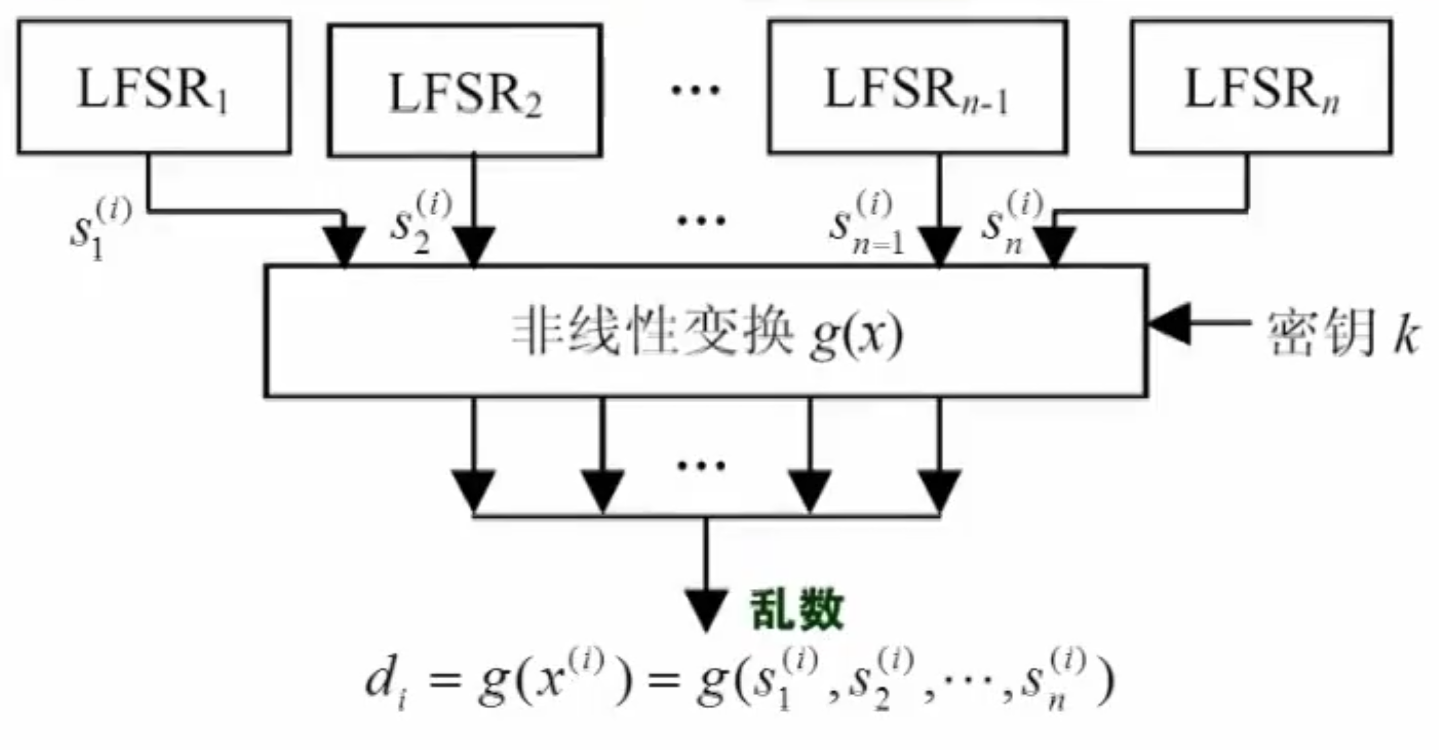
每个 LFSR 为 $g(x^{(i)})$ 提供一个位的输入。只要输入向量序列平衡且周期很大，乱数序列 $d_i$ 也很可能平衡且周期很大。

例：Geffe 生成器

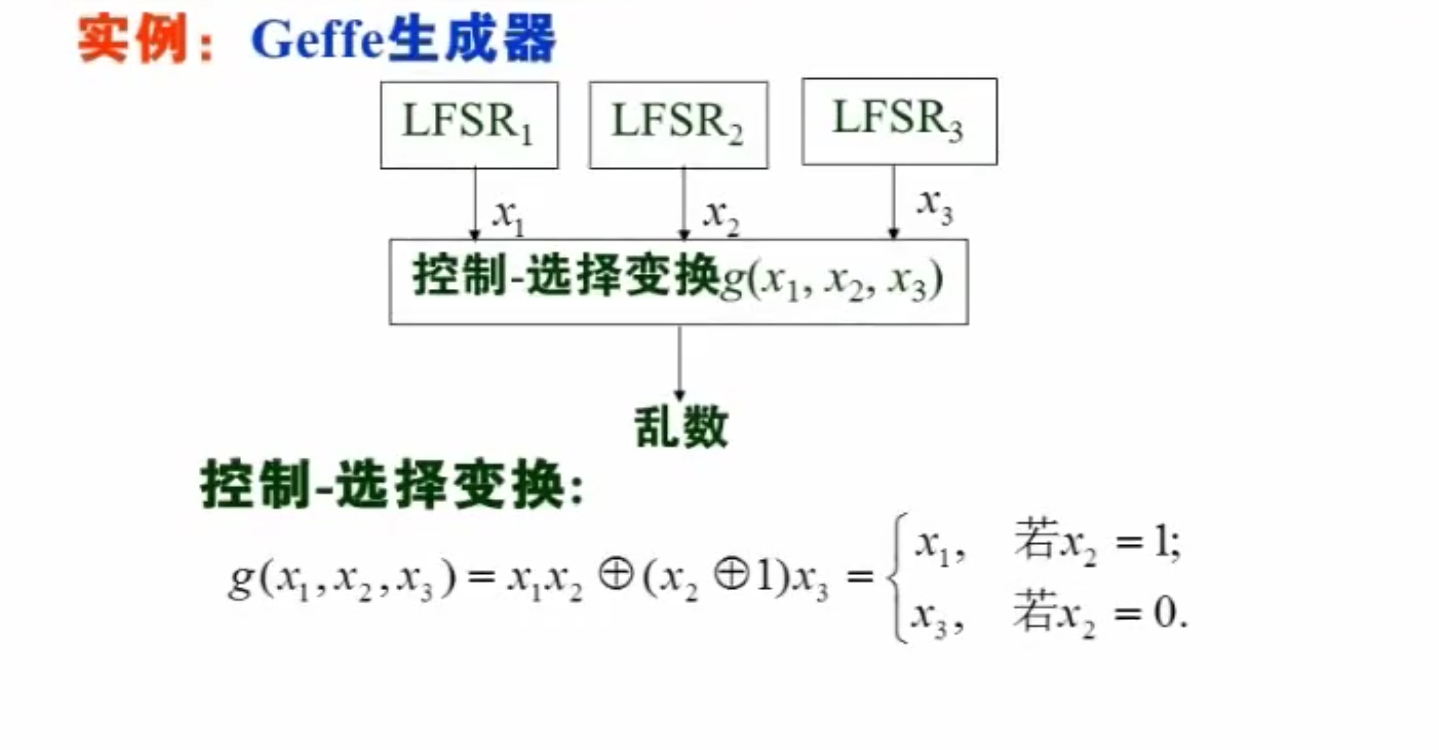
控制-选择变换：通过 $x_2$ 控制输出 $x_1$ 或 $x_3$。

要求：三个输入均为本原且级数互不相同。

该乱数序列是平衡的，且其周期是三个输入 LFSR 的周期乘积。

定理3.5.3

设非线性组合模型由 $n$ 个本原 LFSR 组成，它们的级数 $L_1, L_2, ..., L_n$ 两两不同且都大于 2，其非线性组合函数是代数正规型（二元域上的多元多项式函数表示），表示为 $g(x_1, x_2, ..., x_n）$ 的布尔函数，则乱数序列的线性复杂度为 $g(L_1, L_2, ..., L_n)$。

其中 $g(L_1, L_2, ..., L_n)$ 的运算是将 $g(x_1, x_2, ..., x_n）$ 中的模 2 加和乘法都换成整数～和～。

则 Geffe 生成器的线性复杂度为 $g(L_1, L_2, L_3) = L_1 L_2 + (L_2 + 1) L_3$ 。

代数正规型的计算方法

Boole 函数的代数正规型表示：

$$g(x) = \bigoplus_{a \in Z_2^n} c_a x^a \overset{定义}{=} \bigoplus_{a \in Z_2^n} c_a x_1^{a_1} x_2^{a_2} ... x_n^{a_n}$$

$其中 \forall a = (a_1, a_2, ..., a_n) \in Z_2^n, c_a \in \{0,1\}, x_1^{a_1} 是 x_1 的 a_1 的次方$。

$g(x) 的次数（使得系数 c_a \neq 0 的最大的 a）$：

$$\max \{ wt(a): a \in Z_2^n 且 c_a \neq 0 \}$$

向量 $a$ 的重量：

$$wt(a) = a_1 + a_2 + ... + a_n$$

定理3.5.4

设 $g(x)$ 是代数正规型表示，定义 $x \& a = (a_1 x_1, a_2 x_2, ..., a_n x_n)$ （逐比特与运算）。则 $\forall a \in Z_2^n$ 都有

$$c_a = \bigoplus_{x \in Z_2^n 且 x= x \& a} g(x)$$

特别地，有

$$c_{11...1} = \bigoplus_{x \in Z_2^n 且 x= x \& a} g(x)$$

再限定 $x 的第 k+1, k+2, ..., n 分量全是 0，则 g(x) 退化为一个 k 元布尔函数$

$$f(x_1, ..., x_k) = g(x_1, ..., x_k, 0, 0, ..., 0)$$

（等价于$x = x \& (1, ..., 1, 0, ..., 0)$ ）

此时，$c_{11...10...0} 就是 k 元布尔函数 f(x_1, ..., x_k) 最高次项的系数。$

推论

设 $n \ge 2$，且 $n$ 元 Boole 函数是平衡的，则其次数 $\le n - 1$。

分割攻击

先攻击一部分密钥比特，再借此攻击其他密钥比特。

相关攻击

借助乱序与部分 LFSR 输出序列之间的相关性，先攻击一个或数个 LFSR 的初态，然后再借此攻击其他 LFSR 的初态。

例：分割攻击 Geffe 生成器

$若相等个数 n 比总信号个数 N， \frac{n}{N} \approx \frac{3}{4}，则为初态；若 \frac{n}{N} \approx \frac{3}{4} 则不为初态。$

如何对抗这种攻击？

使少量 LFSR 输出与乱数不存在相关性（相互独立）。

m阶相关免疫函数

定义3.5.3

$设 f(x_1, x_2, ..., x_n) 是一个 Boole 函数， X_1, X_2, ..., X_n 是相互独立且都服从均匀分布的二元随机变量。若 f 对任意 m 个不同的随机向量(X_{i_1}, X_{i_2}, ..., X_{i_n})独立，则 f 是 m 阶相关免疫函数。$

其本质在于不可能利用输出获取任何 $m$ 个输入变量组的信息。

例： $n-1$ 阶免疫函数

$$f(x_1, x_2, ..., x_n) = x_1 \oplus x_2 \oplus ... \oplus x_n$$

定理3.5.4

$n 元 Boole 函数 f(x) 是 m 阶相关免疫函数\Leftrightarrow 对重量 \le m 的二元非零向量 a，都有$

$$W_{(f)}(a) = 0$$

（实际上也$= p(f(X) \oplus a \cdot X = 0) - p(f(X) \ oplus a \cdot X = 1$) 取零概率减取一概率，用全概率公式可转 Walth 谱）

定理3.5.5

$设 n 元 Boole 函数 g(x) 是 m 阶相关免疫函数，则 g(x) 的次数 \le n - m；又若 g(x) 为平衡函数，则当 m \le n - 2，g(x) 的次数 \le n - m -1$。

证明上，令 $t = n-wt(a)$ 即 $x$ 中 0 的个数，$wt(a) > n - m，故 t < m$，则 $c_a = [2^{n-t} p(g(\xi) = 1| \xi_1 = \xi_2 = ... = \xi_t = 0)]mod2 = [2 * \#\{ x \in Z_2^n : g(x) = 1, x_1 = x_2 = ... = x_i+1 = 0 \}]mod2 = 0$。