Diff-Hellman密钥交换

视频

有限域上的离散对数问题

定义

设 $F$ 是一个有限域，则在已知 $F$ 中的元 $a,b$，求解整数 $x$，使得

$$a^x = b$$

在有限域 $F$ 中成立的问题。

它是求 $\log$ 问题吗？ 不尽然，因为必须在域 $F$ 中，且为整数。

其难解性与大合数分解基本相当。

本原元

设 $p$ 是素数，则 $Z/(p)$ 构成有限域，因而其非零元全体按模 $p$ 乘法运算构成循环群。

设 $a \in \{ 1, 2, 3, ..., p - 1 \}$，如果存在 $t$ 使

$$\min \{ t > 0: a^t = 1 \} = p - 1$$

则称 $a$ 是 $Z / (p)$ 的本原元。

有特性 $Z / (p) = \{ 0, a, a^2, ..., a^{p-1}=1 \}$ （任意数可用 $a$ 的幂表示）

Diffie-Hellman 公钥体制

参数选取

选取大素数 $p$，再选取 $Z / (p)$ 的一个本原元 $a$，并将 $p,a$ 公开。

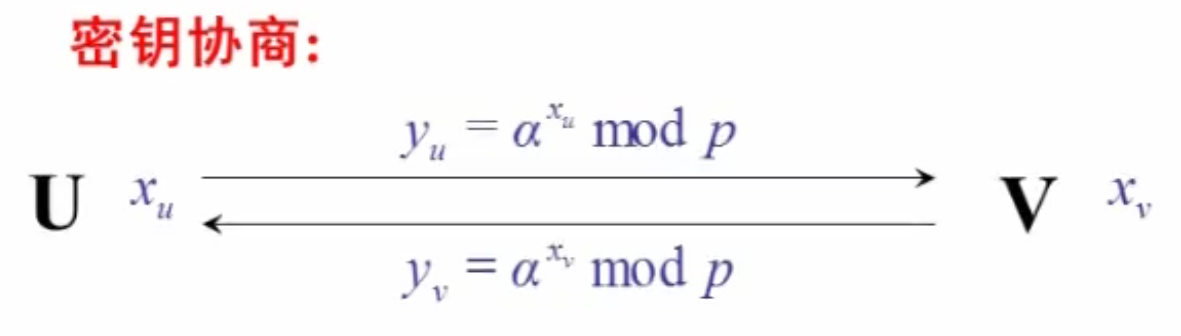
于是可以得到协商的共同密钥 $k$

$$k = (y_v)^{x_u} \mod p = (y_u)^{x_v} \mod p = a^{x_u x_v} \mod p$$

其中，$x_u, x_v$ 都 $1 \le$ 且 $\le p - 2$

（为什么？本原元阶为 $p - 1$，所以大于 $p - 1$ 的数都可以用更小的数取代）

优点

1. 任何两个人都能够协商出一个共同的会话密钥，不需要事先拥有对方的任何（公开、秘密）信息。

2. 每次密钥交换后无需再保留秘密信息，减少保密负担。

缺陷

1. 易受中间人攻击。（与双方身份信息无关，故加上身份信息即可缓解）

ElGamal 公钥体制

也是基于有限域上的离散对数问题，在Diffie-Hellman体制上做出了修改。

参数选取

1. 第一步与 Diffie-Hellman 相仿。

选取有限域 $GF(q)$，再选取上面的一个本原元 $a$，并将 $GF(q), a$ 公开。

随机选取整数 $d: 1 \le d \le q - 2$，并计算出 $\beta = a^d$。

2. 直接将 $\beta$ 作为公开加密密钥，将 $d$ 作为保密的脱密密钥。

明文空间：$M = GF(q) \setminus \{ 0 \}$

密文空间：$M \times M = \{ (x, y): x, y \in M \}$

加密

对 $m \in GF(q) \setminus \{ 0 \}$，秘密选择一个随机整数 $k: 1 \le k \le q - 2$，则密文 $c = (c_1, c_2) \in M \times M$，其中

$$c_1 = a^k \qquad 和 \qquad c_2 = m \beta^k = m (a^d)^k$$

脱密

对任意密文 $(c_1, c_2) \in M \times M$，计算明文

$$m = c_2(c_1^d)^{-1} \\ \qquad = c_2 [(a^k)^d]^{-1} \\ \qquad = c_2 [(a^d)^k]^{-1} \\ \quad = c_2 (\beta^k)^{-1} \\ \qquad = m \beta^k (\beta^k)^{-1}$$

总结

加密密钥 $\beta^k = (a^d)k$，而 $a^k$ 每次加密时临时生成，也不需要每次发送给对方。实质上为一次一密，安全性较高。