椭圆曲线群
定义
- 设 是一个域,,则(基)域 上的椭圆曲线是由(Weierstrass 方程)
和另一个点(无穷远点) 构成的集合,即
其中,Weierstrass 方程也可以用其他椭圆曲线方程取代,例如蒙哥马利方程。
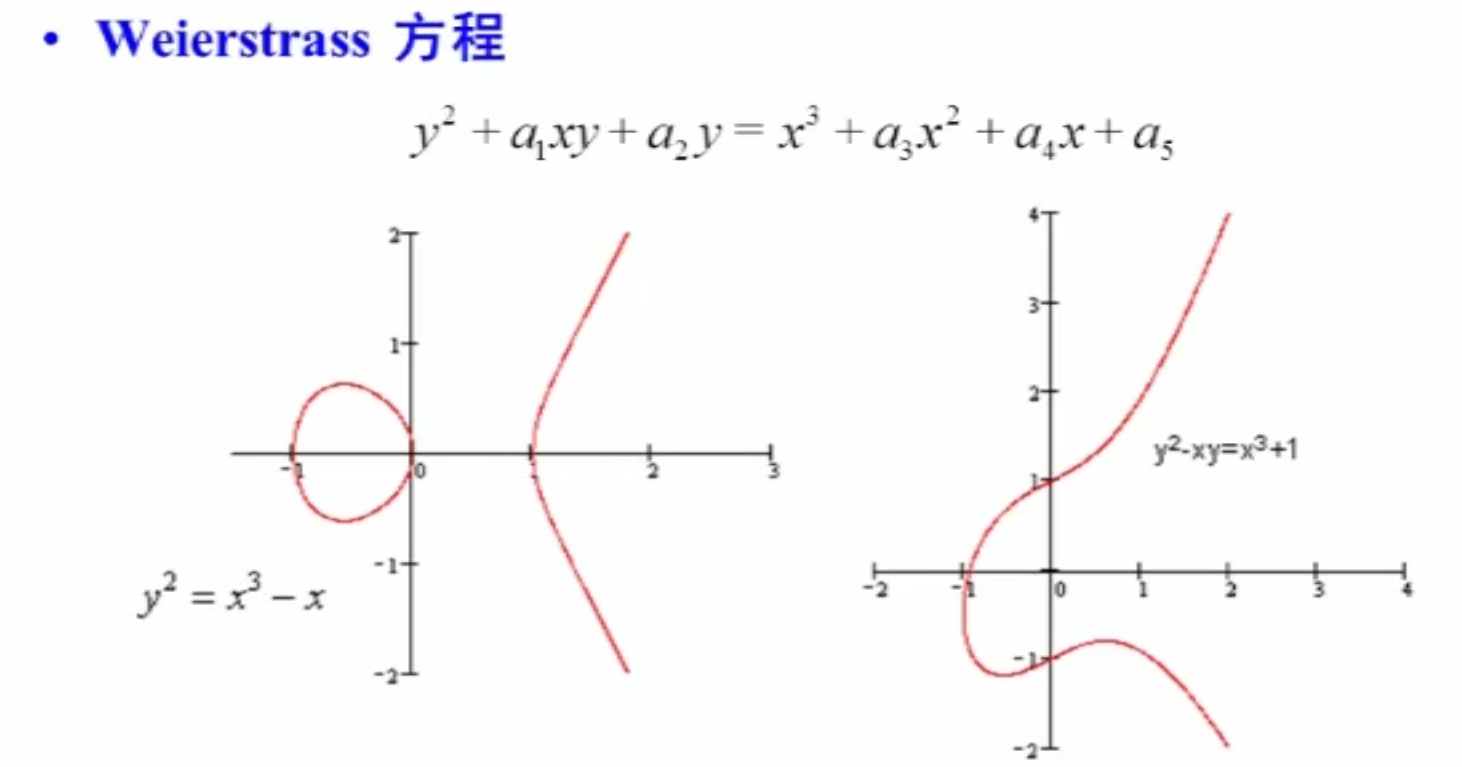
- 设 是一个域,,则域 上的椭圆曲线 是由满足 上的方程 的所有点
和另一个点 构成的集合
该椭圆曲线的判别式为 (一般要求 )。
- 令 是曲线 上的一点,若:
则称点 在曲线 上是奇异的。如果曲线上至少有一个奇异点,就是奇异曲线。
由定义 1 定义的椭圆曲线奇异 。
- 设 是有限域 上的椭圆曲线, ,若
则称 为点 的阶,记为 。
由阶为 的点 在加法定义下生成的循环群 是椭圆曲线群 的一个 阶子群。
- 椭圆曲线群上的离散对数问题
设 是有限域 上的椭圆曲线, 是 的一个循环子群,点 是 的一个生成元,即 ,在已知 的条件下,求解整数 使 。
加法(弦切法)
已知曲线上的点 ,且都不是无穷远点,令 ,则
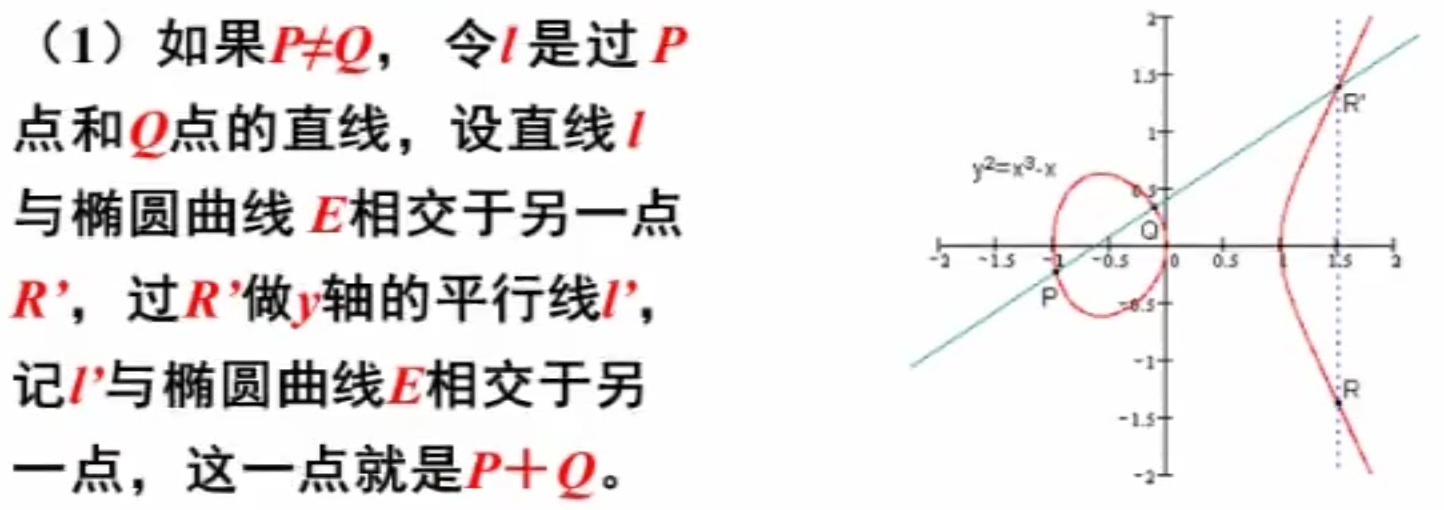


定义:
-
对 ,定义 ;
-
,定义
其中

计算点乘运算可以拆分成点加和倍乘运算。
定理:椭圆曲线按定义的加法运算构成交换群 , 就是该群的零元。
例
- 例

当有限域特征为 时,可将椭圆曲线化为标准型:
当有限域特征 时,可将椭圆曲线化为标准型:
密码学中一般使用以上标准型。
- 例

除法当作乘除数逆元即可。
ECC 椭圆曲线公钥密码
利用椭圆曲线群一个阶很大的循环子群代替有限域的乘法群进行构造,并将阶作为本原元。
参数设定
-
构造有限域 。
-
生成域 上的椭圆曲线 。
-
取椭圆曲线中的一个点 (阶足够大,且生成循环群 中的离散对数问题难解)。
-
选择加密密钥 和 解密密钥 ,使 。(类似与 Elgamal 的 )
公开
加密
选择随机
已知明文
计算密文
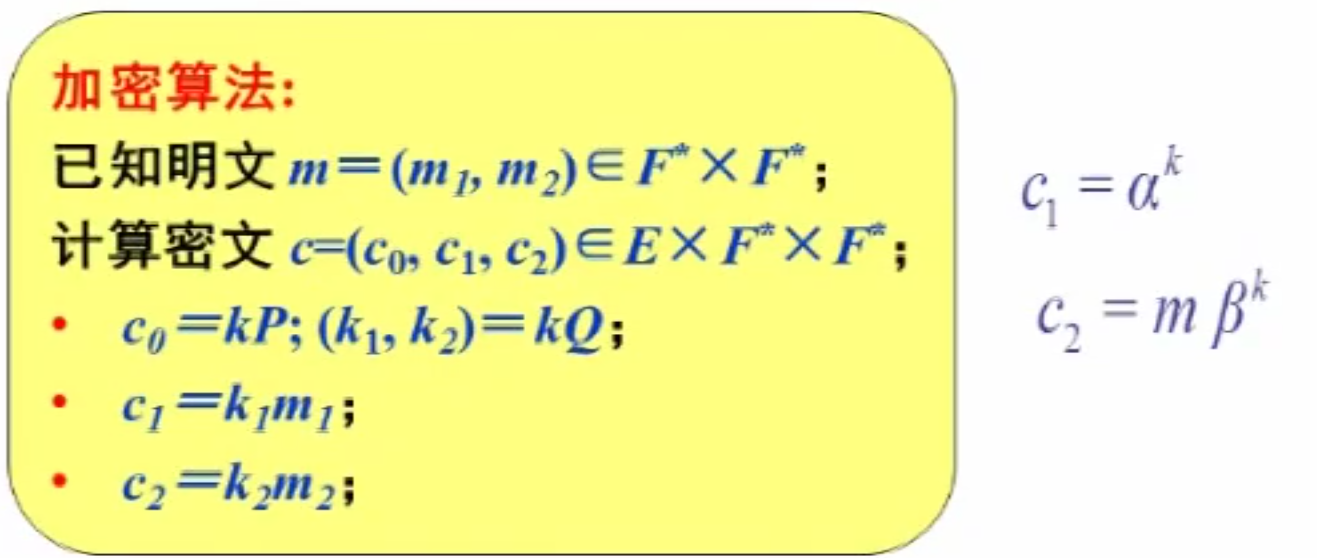
将 Elgamal 有限域中的数化为群中的点。
脱密

