杂凑函数基础
杂凑函数(aka 哈希函数、报文摘要函数、散列函数等),是将任意长度的报文 压缩成固定长度的报文摘要 的函数。
有两种杂凑函数,不带密钥的(MDC)、带密钥的(MAC)。
特性
- 单向性(求第一原像不可行)。 可求,反之计算不可行。
- 弱无碰撞性(求第二原像不可行)。任意给定报文 找出另一个不同报文 使得 计算不可行。
- 强无碰撞性。任意两份报文杂凑值不同。
应用
- 完整性检验。
- 数字签名。
- 密钥推导。
- 伪随机数生成。
自由起始碰撞攻击
目的是找到两个不同的 使得 。
步骤
- 随机选取 个不同报文
- 计算这 个报文的杂凑值,得到集合
- 根据 的大小,对集合 快速排序
- 若过程中找到两个不同消息使 就成功停止,否则失败停止
指标分析
所需存储量:表 的规模
所需计算量:
- 生成集合 的计算量为计算 次杂凑函数
- 快速排序并找出碰撞的计算量为 次比较
成功率:
定理1
设杂凑值为 bit 且 远小于 ,则碰撞攻击的成功率近似为
特别地,当 时,碰撞成功率近似为
特别地,当 时,碰撞成功率近似为
对该定理的推导

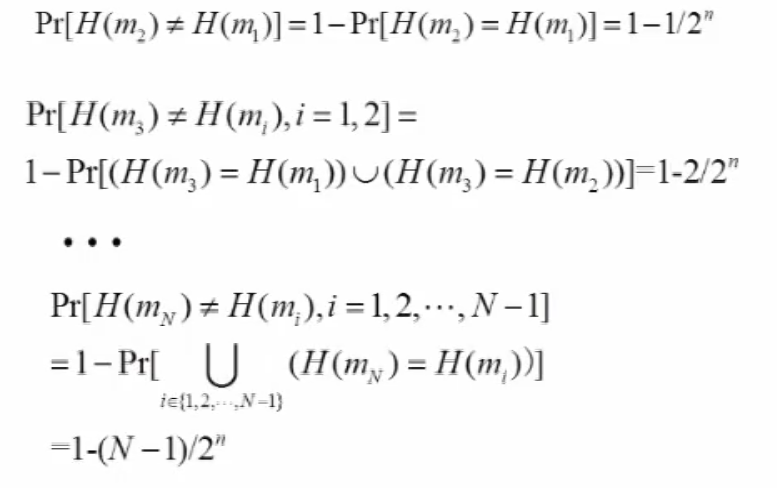
所有 都不相同,完全没有碰撞的概率为
由 有(没有学过数分不懂,只能记结论)
结论
假设能对抗穷举攻击的密钥长度安全界限为 ,能够对抗碰撞攻击的杂凑函数安全界限为 。
基于分组密码的杂凑函数
Merkle-Damaard 强化技术
将消息 的最后一个分组 设置为原始消息长度。
这样,。
基于分组密码设计杂凑函数的一般方法
消息 ,初始值 ,,最后得到 就是消息的杂凑值。也就是不断 update 初值至完整消息。
常见的杂凑函数设计如下
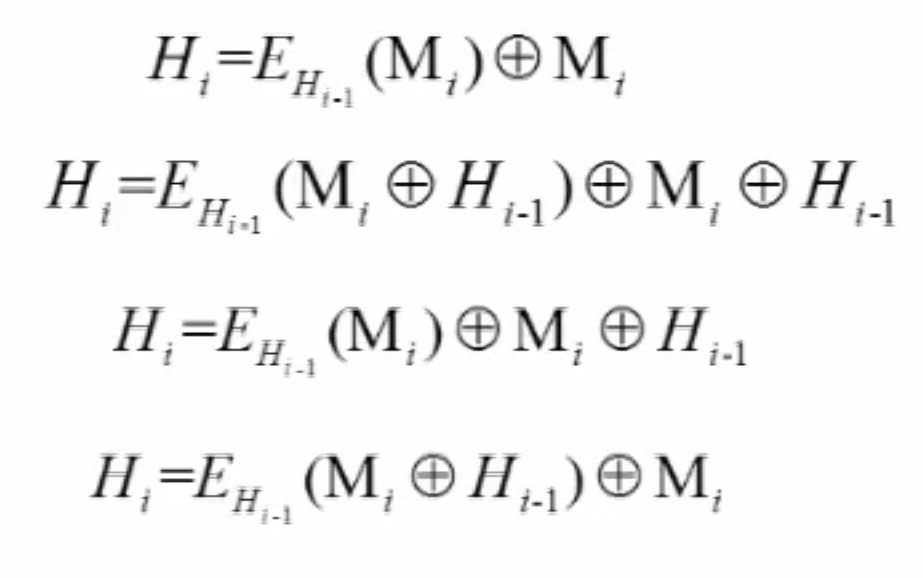
MD5
由 MD4 改进,产生 128 位输出,一个主循环处理 512 bit(长度 ,执行次数 )
初始化
- 原始消息二进制后填一个 1,然后在最低 64 bit 填入原始消息长度的二进制,中间全部补 0,填充后长度为 512 bit 整数倍。长于 时,模 直接填入后 64 bit。
- 将填充后结果 分为 个 512 bit 块
- 将每个块 再划分为 16 个 32 bit 的子块,记为
初始向量
- A = 0x01234567
- B = 0x89abcdef
- C = 0xfedcba98
- D = 0x76543210
基本函数

过程
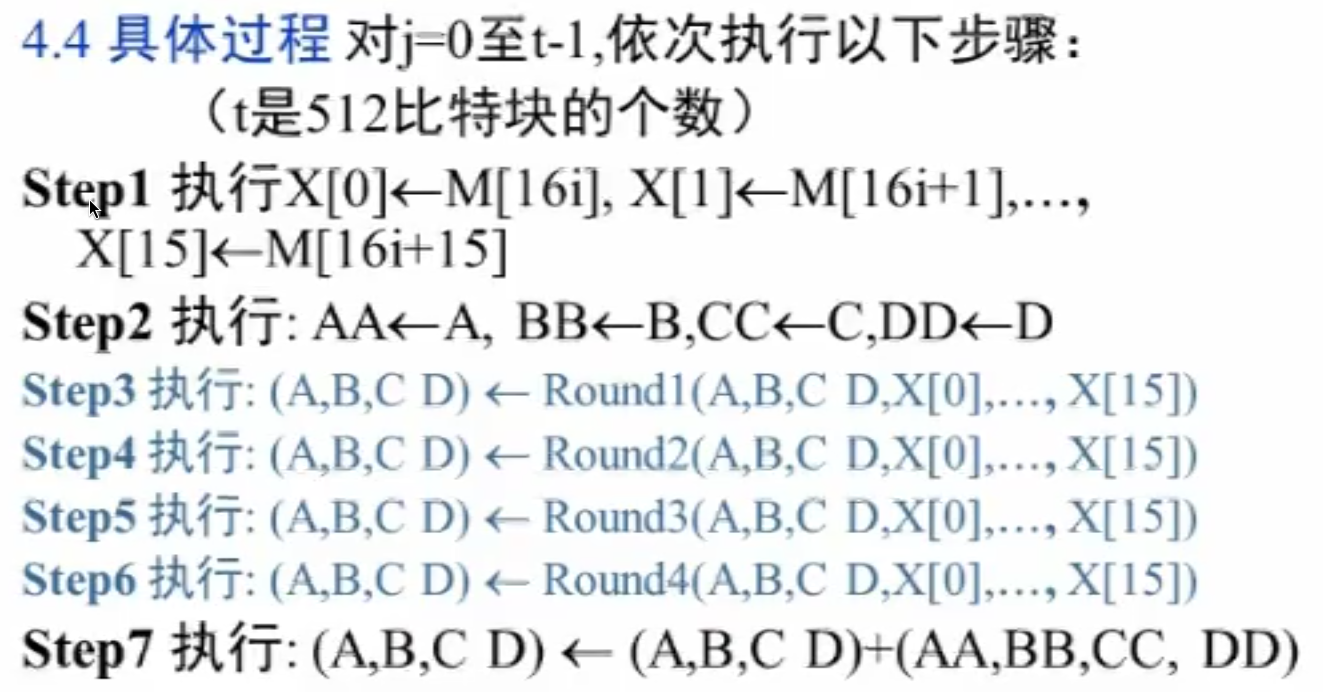
- 将 16 个子块放入缓存
- 保存初始值为
- 数据块与 刷新多轮
- 结果与原始值模 加(如 )
连接最后输出就是结果。

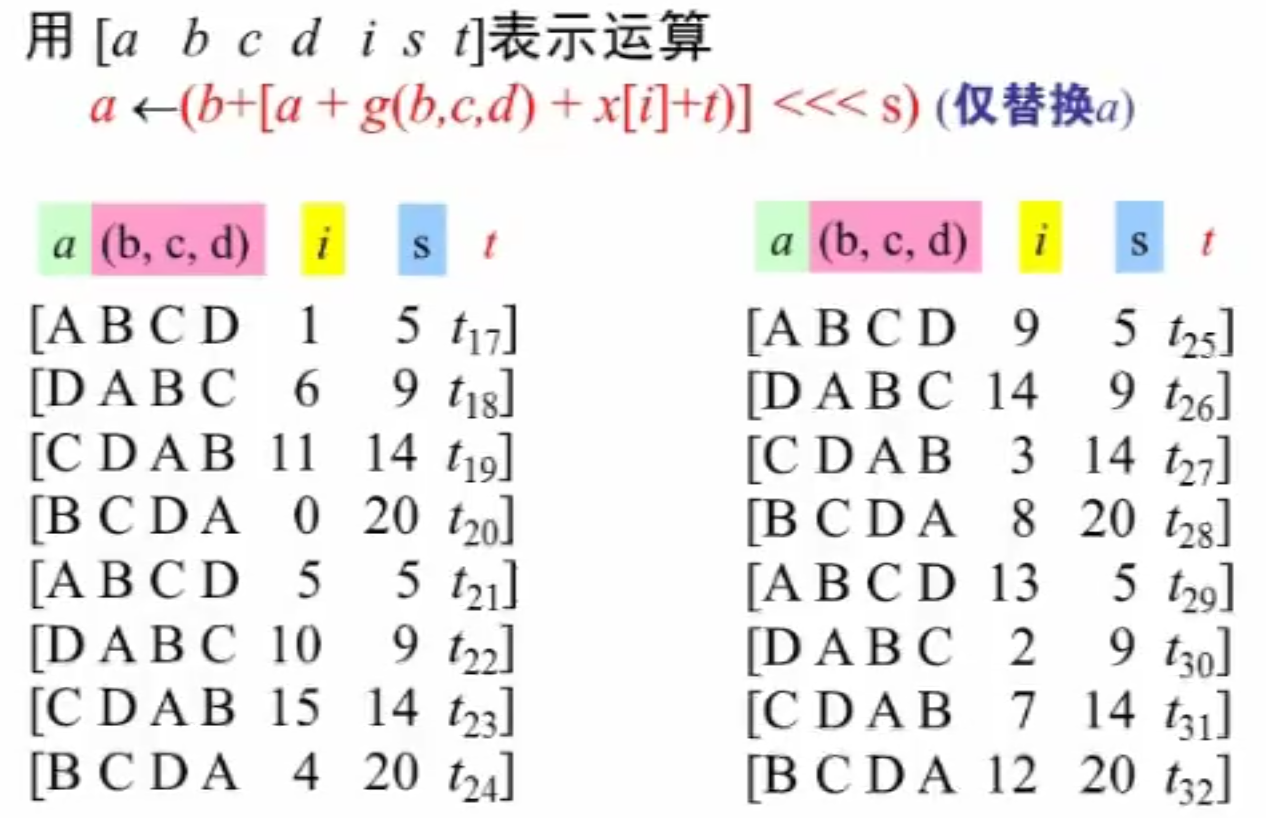
第二轮也是类似,将 变为 。之后每一轮也是更换一个函数。
安全性
MD5 算法已被证明是不安全的。
SHA-2
以 SHA-512 为例。
初始化
- 原始消息二进制后填一个 1,然后在最低 128 bit 填入原始消息长度的二进制,中间全部补 0,使得填充后长度是 1024 整数倍。长于 时,模 直接填入后 128 bit。
- 将填充结果分为 8 个 64 bit 块。
也有很多很多的初始向量,记忆这些东西没有意义,略过。
基本函数
过程
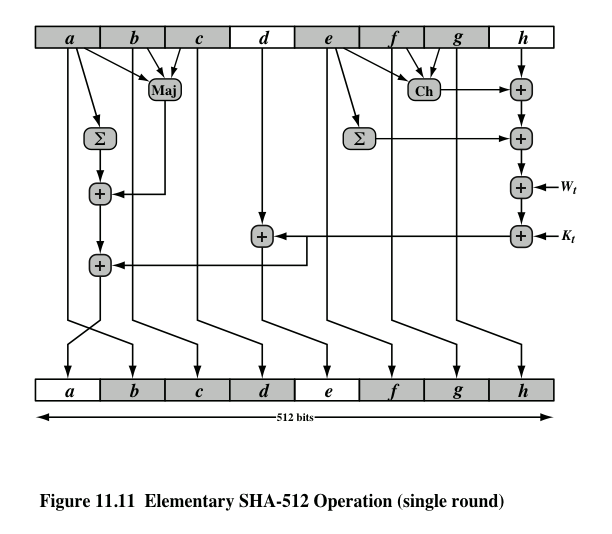
计算最终结果
拼接
SHA-3
基于海绵函数,我搞不懂。
基于杂凑函数的消息认证码
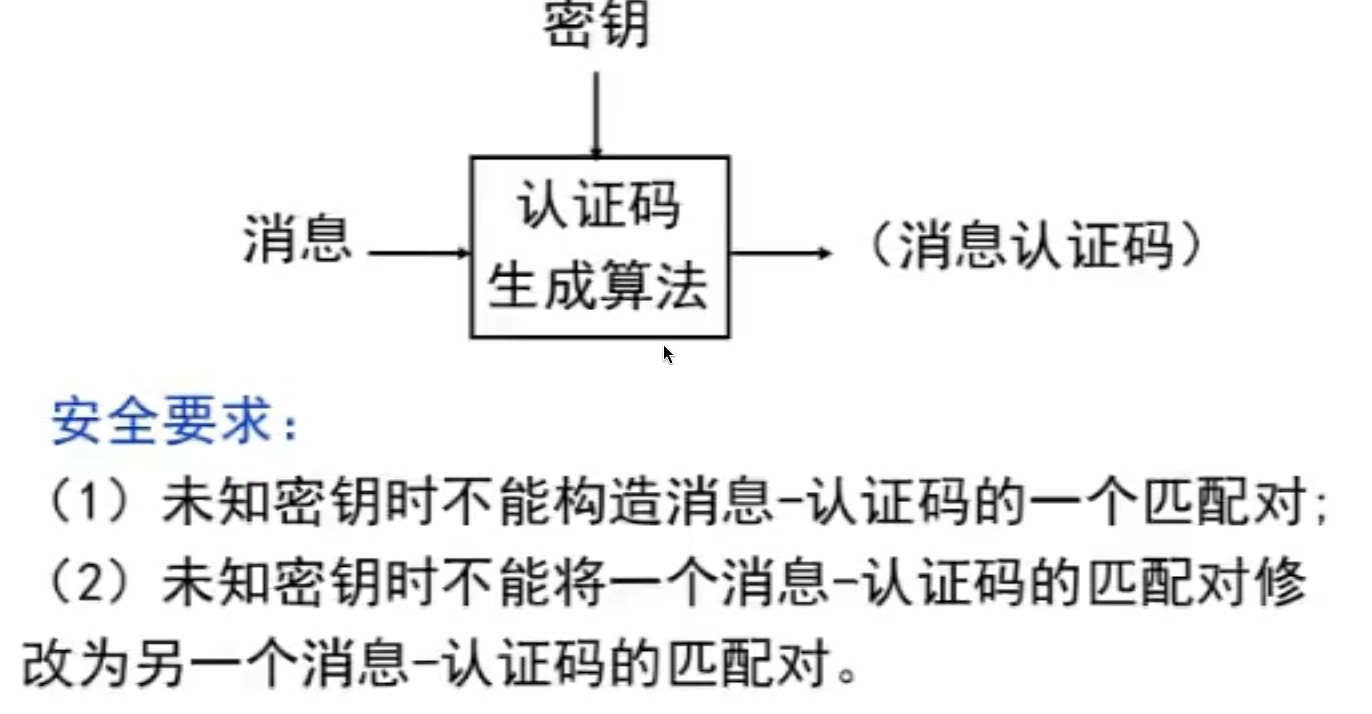
基于杂凑函数的 HMAC 消息认证码
有密钥 函数 ,两个包含 信息的数字串 ,计算消息 的认证码:

